В рамках глобальних напрямків дослідження велися в наступних конкретних напрямках:
Фізичні ефекти, явища та закономірності
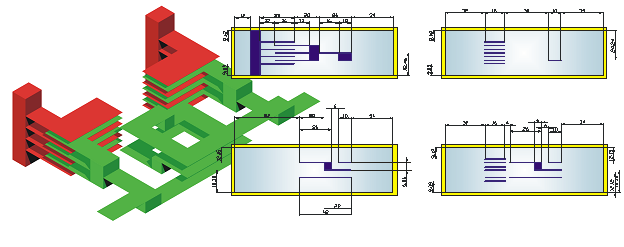
В задачах розсіювання хвиль на гратках знайдені глобальні закономірності, що витікають з загальних законів електродинаміки ‑ зокрема, доведено факт незалежності коефіцієнта відбиття в основний порядок від знака кута падіння для решіток довільного профілю [1]. Цей факт породив ряд неочевидних наслідків, як наприклад, повне проходження Н- поляризованої плоскої хвилі крізь гратку типа «жалюзі» не тільки в тривіальному, але і в «нетривіальному» випадках (Рис.1а), повне автоколімаційне відбиття від ешелету у таких же саме двох випадках (Рис.1б), незалежність втрат на випромінювання модульованого пучка електронів над періодичною структурою від знака напрямку руху тощо. Як важливі для застосування в техніці антен і в квазіоптиці, досліджено явища несиметрії розсіяного поля при дифракції на гратках «жалюзі» і ешелет, особливості розсіяння на різноманітних стрічкових гратках, в тому числі із покриттям, явища недзеркального відбиття (до повного перетворення в хвилю вищого порядку включно), явища перетворення та поглинання хвиль на багатошарових схрещених гратках. При цьому виявилося можливим забезпечити як вузькі, так і широкі смуги частот, знайти об’єкти, що мають поляризаційну відбірковість, або ефекти, що є характерними для обох поляризацій падаючого поля тощо.
Ці дослідження, виконані на точних «теоретичних» моделях породили, тем не менше, ряд «конкретних застосувань» в техніці антен та квазіоптиці.
 |
| Рис .1 Тривіальні та нетривіальні випадки розсіювання на несиметричних решітках |
Розпочавшись з аналізу причин засліплення ФАР із покриттям і перетворювачів поляризації, були широко поставлені дослідження резонансних явищ при дифракції на періодичних структурах, резонансів на «замкнених» Флоке- та хвилеводних модах, в багатоапертурних перфорованих екранах тощо. «Виходом у практику» тут явилися нові конфігурації відкритих резонаторів із спеціальними дзеркалами, нові типи частотно- і кутоселективних фільтрів, решіток-перетворювачів поляризації. Цикл робіт з розсіювання хвиль на періодичних структурах знайшов узагальнення в монографії [2] і продовжується в теперішній час (А.О.Кириленко, Л.А.Рудь, Ю.К.Сіренко, С.Л.Сенкевич та Л.П.Мосьпан). Як приклад застосування резонансних ефектів нового типу, вкажемо на роботу [3], де запропоновано використовувати перфоровану стрічкову решітку в якості вузько-смугового відбивача. (А.О.Кириленко, Л.П.Мосьпан).
Встановлено ряд нових закономірностей розсіювання хвилеводних хвиль, що носять загальний характер і суттєво доповнюють відомі закони взаємності та збереження енергії. Показано, наприклад, що розподіл потоку вектора Пойнтінга при розсіюванні на симетричних хвилеводних перешкодах також симетричний. На цій основі знайдені співвідношення, що пов’язують амплітуди і фази не лише основних, але і вищих затухаючих хвиль, що дало додатковий апарат для контролю чисельних моделей хвилеводної електродинаміки.
 |
| Рис.2 До ефекту повного відбиття перед точкою виникнення вищої хвилі |
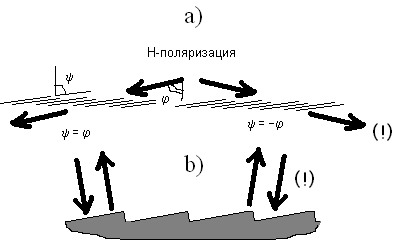
До числа загальних законів належить і закон «повного запирання тракту поблизу верхньої точки одномодового діапазону «малими електричними розширеннями», викликаними нерегулярністю зі зміною перерізу або заповнення (Рис.2). Виявлене в 50-х роках минулого століття Б.З. Каценеленбаумом на малих зламах хвилеводу, це явище, як виявилось, носить загальний характер і характерно для будь-яких слабких розширень хвилеводного тракту (власно хвилеводу або каналу Флоке). Серед них власне стрибки поперечного перерізу, діелектричні вставки з похилими межами або вставки з близько розташованою неоднорідністю, періодичні гратки поблизу тонкого шару діелектрика тощо (А.О.Кириленко, Л.А.Рудь, В.І.Ткаченко, Т.І.Васильєва, О.П.Кусайкін, І.С.Цаканян, С.Л.Сенкевич).
Співробітники відділу стали піонерами в строгому аналізі кутових неоднорідністей в прямокутних хвилеводах, в наслідок чого отримано перші вирішення найважливіших практичних завдань синтезу невідбиваючих куточків, переходів і розворотів в одномодових хвилеводах, знайдені деякі нові корисні ефекти. Виявлено, наприклад, що 135° – куточок може забезпечити унікально високе узгодження (КНВ<1.005) у всьому робочому діапазоні хвилеводу. При аналізі куточкових елементів в багатомодових хвилеводах знайдено нетривіальні ефекти перетворення хвиль, що відкрили шлях до синтезу унікальних за простотою конфігурацій збудників вищих TEq0-хвиль (2≤q≤20). Останні дали ключ до створення відповідних ділильників потужності на 2÷10 каналів [4]. Перетворювач TE10⇔TE60зображений на Рис.3.
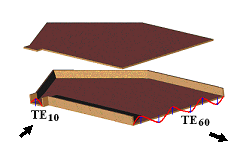 |
| Рис.3 Перетворювач типів мод H10⇔H60 |
Виявлено, досліджено теоретично і підтверджено експериментально ефект частотного сканування діаграми спрямованості двохпелюсткової рупорної антени, що базується на „підмішуванні” TE10-хвилі на виході куточкового збудника TE20-хвилі.
Дослідження з хвилеводного розсіювання знайшли узагальнення в монографії [5] і продовжуються на даний час (А.О.Кириленко, Л.А.Рудь, В.І.Ткаченко, С.Л.Сенкевич).
За роботи в галузі «теорії резонансного розсіювання хвиль та її застосування в радіофізиці» доктори наук А.О. Кириленко, С.О. Масалов, Л.А.Рудь та Ю.К.Сіренко стали лауреатами Державної премії УРСР в галузі науки та техніки 1989 року.
У відділі закладено основи спектральної теорії структур із дискретним просторовим спектром (хвилеводів та періодичних структур). Було знайдено зони існування і локалізації спектрів комплексних власних частот, загальні і частинні (для конкретних класів відкритих структур) закономірності їх поведінки при зміні параметрів, ефекти повного перетворення, поглинання і проходження пакетів хвиль, відповідні спектральним точкам на реальній вісі віщих листів Ріманової поверхні тощо [6,7] (Ю.К.Сіренко, Л.А. Рудь, Н.П. Яшина).
Найважливішим результатом стало встановлення аналітичних співвідношень, що пов’язують елементи матриць із спектрами комплексних власних частот і які перекидають «місток» між «суто умоглядними» уявленнями спектральної теорії і «реальними» явищами розсіювання. На цій основі, зокрема, вдалося дати нову інтерпретацію класичних резонансів на «замкнених» модах, як відгук на пакет власних коливань (добротних і недобротних), а не тільки на одне з них, як вважалося раніше [8] (А.О.Кириленко, Б.Г.Тисік). Значно пізніше, це підштовхнуло до створення нових типів режекторних фільтрів на багатоапертурних діафрагмах і найпростішої конструкції хвилеводного режекторного фільтру «на стрічці із щілиною» [9] (А.О.Кириленко, Л.П.Мосьпан).
Виявлено якісно новий тип «понаддобротних» коливань відкритих хвилеводних об’єктів, коли відсутність втрат на випромінювання пояснюється не тривіальними причинами, такими як відсутність самого зв’язку резонуючого коливання з вихідними хвилеводами (внаслідок симетрії або позамежності), а «інтерференційним гасінням» випромінювання різних мод у вихідні хвилеводи [10] (А.О.Кириленко, С.Л.Сенкевич, Б.Г. Тисік, Л.П. Мосьпан).
Побудовано наближені і точні чисельні моделі резонансного поглинання енергії у хвилеводно-діелектричних резонаторах (ХДР), що пов’язують дифракційні і поглинаючі властивості ХДР з характеристиками власних коливань ХДР. Відоме уявлення про максимально можливий рівень поглинання (до 50%) при порушенні ізольованого коливання було істотно розширено виявленням ефекту повного поглинання в одиночних багатомодових ХДР. Останній проявляється на частоті, близької до частоти виродження двох власних коливань, що мають різну симетрію уздовж вісі резонатора і близькі добротності [11]. Аналіз резонансів вищих коливань у діелектричних резонаторах з некоординатними межами дозволив запропонувати новий засіб вимірювання параметрів діелектриків, що слабо поглинають, заснований на вирішенні оберненої задачі відновлення параметрів матеріалу за частотою і добротностю резонансу вищого коливання яке має мінімальні втрати на зв’язок (Л.А. Рудь, А.О. Кириленко, Т.І. Васильєва).
Під час дослідження явищ розсіяння на плоских решітках із неідеальних тонких стрічок було виявлено близьке за природою резонансне поглинання хвиль поблизу точок ковзання просторових гармонік вищих типів (наприклад, на верхній межі одномодового діапазону) (А.Й.Носич) [12].
Задачі дифракції та поширення хвиль у відкритих хвилепровідних та резонансних структурах з безперервним просторовим спектром
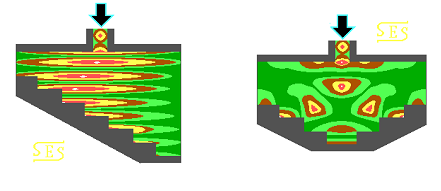 |
| Рис .4 Поля коливань ешелетних та куточково-ешелетних коливань, знайдені за допомогою хвилеводних моделей СЭМ-04 |
Широкий розвиток робіт по вакуумним і твердотілим міліметровим генераторам, що використовують відкриті резонатори, у відділах В.П. Шестопалова і Б.М. Булгакова породив потребу в чисельному моделюванні, яке забезпечує повний електродинамічний аналіз таких резонаторів, що включає пошук спектрів коливань, можливостей їх розрідження та вибір пристроїв зв’язку. Одним із яскравих прикладів застосування таких моделей стало дослідження електродинаміки відкритих резонаторів з «дисперсійними» (ешелетними, куточково-ешелетними та ін.) дзеркалами, що дало перший приклад аналізу «квазіоптичних» об’єктів на строгих і точних моделях і було виконане в співдружності з відділом твердотільної електроніки (див. Рис. 4) [13] (А.О. Кириленко, В.І. Ткаченко, А.І. Фісун, О.І. Білоус).
Великий цикл робіт з відкритих хвилеводів (ВХ) і резонансних систем був реалізований під керівництвом А.Й. Носича. Було розвинено елементи теорії збудження хвиль в ВХ та обгрунтовано умови випромінювання для вирізнення єдиних рішень відповідних задач, що відрізняються від умов випромінювання Зоммерфельда і Свєшнікова [14].
В конкретних роботах велика увага приділялася розробці методів аналітичної регуляризації заснованих, наприклад, на зверненні статичної частини оператора задачі (ідеально провідні незамкнені циліндри в шаруватому середовищі, періодичні решітки, плоскі та сферичні диски з ідеальних або неідеальних елементів тощо) або на обертанні оператора деякої частини геометрії (у задачах дифракції хвиль на діелектричних циліндрах довільної форми). У задачах моделювання квазіоптичних антен (дзеркальних і лінзових) було використано нові прості засоби опису апертурного випромінювача, як джерела, яке розташоване в точці з комплексними координатами.
Виявлено ряд антенних ефектів, цікавих з практичної точки зору: Продемонстровано, наприклад, що деякі з резонансів радіолокаційного перерізу розсіювання можна пригнічувати за допомогою тонких поглинаючих покриттів магнітного типу. Виявилося, що коефіцієнт спрямованості дзеркальної антени можна збільшити за допомогою резонансного обтічника, оптимізуючи його геометричні параметри.
У теорії дуже популярних друкованих антен показано, що в мікросмугових антенах спільно існують резонанси підкладки, смугового випромінювача і власне основи, які потрібно враховувати при їх фізичному аналізі та проектуванні.
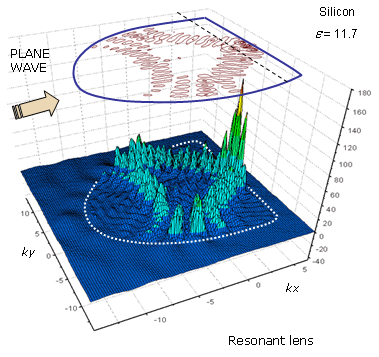 |
| Рис . 5 Поле «напівеліптичної» лінзи при випромінюванні в умовах резонансу |
Велика увага приділялася задачам розсіювання та збудження у присутності однорідних и неоднорідних діелектричних циліндрів різних форм поперечного перерізу. Їх характерною рисою є внутрішні резонанси і здатність служити хвилепровідними системами. Детально вивчено моди шепчучої галереї в циліндрах кругової і некругової форми – їх частоти і добротності, а також вплив на них шаруватості зовнішнього середовища. Було досліджено направляємі, витікаючі і комплексні хвилі у відкритих хвилеводах складної форми, їх дисперсію, власні поля та перенесення енергії включно [15].
Під час дослідження режимів квазіоптичної фокусування і внутрішніх резонансів в однорідних діелектричних лінзах складної форми було доведено, що резонанси відіграють таку значну роль, що дозволяють запропонувати нові принципи проектування лінзових антен. На Рис.5, наприклад, показано, як в резонансних умовах для лінзи складеної з половини еліпсу і прямокутника, резонансні плями поля з інтенсивністю вищою, ніж у її геометричному фокусі, можуть виникнути біля плоского боку. Це вказує шлях до розробки резонансної приймальної лінзової антени з більш високою чутливістю [16,17] (А.Й. Носич, Н.Ю.Близнюк, А.В.Борискін).
Розвиток робіт з моделювання: від окремих програм до систем автоматичного моделювання та проектування
Серед різних шляхів реалізації спільної ідеї виділення та обігу головної частини оператора крайової задачі, що уславила Харківську школу електродинаміки, помітне місце займає метод напівобернення матричних систем рівнянь з різницевим ядром, розвинений співробітниками відділу А.О. Кириленко, Л.А. Рудем, Ю.К. Сіренко спільно с з С.О. Масаловим. Цей метод, детальний виклад якого надан у книзі [18], дозволив отримати перші точні розрахунки для таких класичних структур як ешелетні гратки та злами хвилеводів, забезпечив детальне дослідження різноманітних резонансних явищ, у тому числі в багатомодових хвилеводах. Завдяки високій ефективності чисельних алгоритмів, а потому і можливості застосування процедур оптимізації, цей метод дав розв’язок багатьох практичних задач.
Ускладнення задач, насамперед хвилеводних, вимагало розширення теоретичного інструментарію, що дає основу чисельних алгоритмів і застосування інших чисельно-аналітичних підходів: методу Вінера-Хопфа, методу інтегральних рівнянь, методу часткових областей з урахуванням особливостей поля на ребрах, методу «закорочених портів» і методу «скаляризації» векторних задач, що дозволяють знизити порядок складності ряду задач електродинаміки тощо. Розрахунок композиційно складних об’єктів зажадав широкого використання методу S-матриць і створення «ідеології» електродинамічної збірки, що породила відповідний пакет алгоритмів.
Відмінною рисою робіт по чисельному моделюванню стала особлива увага до швидкодії чисельних моделей, до точності і стійкості результатів, до максимальної уніфікації програм, реалізованих послідовно на Алголі, Фортрані, PL-1 і на С++. Як результат такої «уніфікації», наприкінці 80-х років минулого століття вдалося поставити питання про створення «системи моделювання», що інтегрує зусилля окремих фахівців з розрахунку хвилеводних елементів самих різних класів в потужний теоретичний інструмент аналізу проблем розсіяння в хвилеводах. Для вирішення подібних задач була створена і постійно розширюється бібліотека алгоритмів розрахунку S– матриць ключових елементів: хвилеводних трактів, таких як сходинки і розгалуження, злами і куточки, трійники, хрести та інші багатоплечі з’єднання у прямокутних, круглих та коаксіальних хвилеводах, координатні і некоординатні діелектричні елементи, ступінчасті з’єднання хвилеводів складних перетинів, включаючи П-подібні, хрестоподібні і т.д. Перша система моделювання, яка спирається на чисельно-аналітичні алгоритми розрахунку ключових елементів, була створена наприкінці 80-х років минулого століття, реалізована на мові PL-1 на великих ЕОМ серії ЄС і успішно експлуатувалася в ряді галузевих НДІ МЕП і МРП СРСР під назвою СЕМ-04. У 1990 р. вона була визнана «кращим програмним продуктом» на першому (і, нажаль, останньому) Всесоюзному конкурсі програм у галузі антено-фідерної техніки. (А.О. Кириленко, В.І. Ткаченко).
Досвід, накопичений при розгляді задач методом часткових областей (МЧО), дозволив поставити задачу узагальнення МЧО на довільні структури з кусково-координатними межами. При цьому «довільність» розглянутого об’єкта вимагала створення засобів і методів специфікації його геометрії у вигляді, наприклад, послідовності координат характерних точок, апроксимації некоординатних поверхонь ступінчастими, розпізнавання отриманою просторовою фігурою як набору часткових областей, визначення підобластей їх перекриття тощо. Разом з пакетом алгоритмів, які реалізують операції зшивання полів на межах підобластей і відповідні проекційні операції, отримане «узагальнення МЧО» стало фактично новим обчислювальним засобом, порівняним з сітковими методами по загальності, але що зберігає високу швидкість і точність розрахунків, характерну для МЧО. У 2001-2002 роках на цієї основі було створено дослідну систему моделювання MWD-01, функції інтерфейсу користувача якої базувалися на САПР AutoCAD, що має засоби редагування об’єктів і візуалізації характеристик (від АЧХ до двохвимірних розподілів поля) і призначена для аналізу об’єктів, обмежених «кусочно-координатними поверхнями» в декартовій системі. (А.О. Кириленко, В.І. Ткаченко, Д.Ю. Кулик).
Завдяки новому підходу до чисельної реалізації, вдалося вперше застосувати МЧО в задачах розрахунку багаташарових інтегральних схем [19], що вимагало аналізу хвилеводів найскладнішої конфігурації, які виникають при поперечному «розтині» такої схеми на ряд фрагментів (Рис. 6). З його ж допомогою проаналізовано нові типи фільтрів з резонаторами на відрізках «спіралеподібних» хвилеводів [20], розраховано характеристики магічного «Т» і розв’язано ряд інших задач, які потребували швидкої маніпуляції конфігурацією об’єктів. Один з найбільш вражаючих результатів дала «повна автоматизація» алгоритмів метода часткових областей, що дозволила ставити обчислювальні задачі, які раніше не реалізовувалися у силу їх громіздкості. Виявилося, наприклад, що сферу застосування МЧО, одного із найефективніших методів електродинаміки, можна поширити і на задачі з плавними границями шляхом їх ступінчастої апроксимації, що різко розширює межі його застосування [21,22] (А.О. Кириленко, В.І. Ткаченко, Д.Ю. Кулик).
Проблемно-орієнтовані алгоритми синтезу, аналізу та оптимізації антено-фідерних пристроїв поляризаційної і частотної селекції
Починаючи з 1995 року, у відділі розгорнуто цикл робіт зі створення проблемно-орієнтованих пакетів програм, що забезпечує весь цикл робіт з проектування таких пристроїв як смуго-пропускаючих і смуго-відбиваючих фільтрів з послідовними і перехресними зв’язками, фільтрів нижніх частот, діплексерів, мультиплексерів, подільників і перетворювачів поляризації, гладких и гофрованих рупорних випромінювачів тощо. Фактично мова йдеться про серії САПР, що дозволяють за специфікацією на необхідні «електричні характеристики» отримати геометрію пристроїв, що забезпечує необхідні параметри неузгодженості, позасмугового придушення, розв’язку між частотними або поляризаційними каналами, коефіцієнту эліптичності, рівню крос-поляризації, ширини діаграми спрямованості та ін.
Поряд з вирішенням проблем попереднього синтезу, що зводяться до «відновлення» геометричних розмірів «реальних» елементів радіотехнічного прототипу за вимогами до їх електродинамічних параметрів, було розроблено алгоритми ітераційного уточнення геометрії об’єкту з використанням строгої моделі пристрою в цілому, що враховує частотну дисперсію елементів синтезованого пристрою, взаємодію по ближнім полям, міжмодову взаємодію тощо.
На Рис.7 зображено деякі з частотно-селективних пристроїв техніки НВЧ, які можуть бути синтезовані за допомогою пакетів програм, створених у відділі. Серед них різноманітні смугові фільтри мм та см діапазонів (на рисунку представлені BPF01, BPF02, BPF06), фільтри на затухаючих модах з великою смугою загородження (BPF06), фільтри нижніх частот (LPF01, LPF11), фільтри на ортогональних коливаннях (BPFD01), односмугові і двохсмугові режекторні фільтри (BSF01), діплексери різноманітних типів на трійниках і на розгалуженнях (DEB01, DEТ01, DHT01, DHL01).
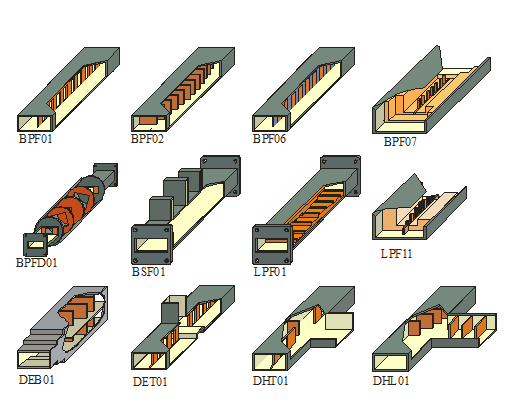 |
| Рис .7. Приклади частотно-селективних пристроїв НВЧ діапазону та імена відповідних САПР |
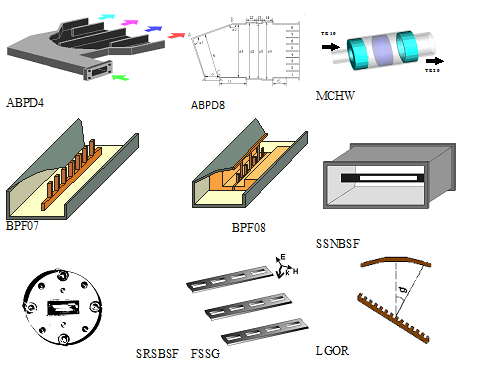
Крім вузлів частотної селекції розроблялося і програмне забезпечення для аналізу та синтезу багатьох інших антено-фідерних вузлів таких, як ступінчаті переходи з прямокутного на круглий хвилевід (RCT) односмугові і двохсмугові збудники хвиль кругової поляризації (SPTA), випромінювачі антен кругової поляризації на гофрованому рупорі (CСHA), роздільник сигналів лінійної поляризації (NBOMT), спрямований відгалужувач на хрестоподібних щілинах (CSMC), гермовікна у хвилеводах різних типів (DHWR) (Рис. 8)
 |
| Рис.8. Приклади антено-фідерних пристроїв НВЧ діапазону і імена відповідних САПР |
Хоча основна «спеціальність» відділу полягала в розробці обчислювальних методів і засобів, колектив відділу запропонував і дослідив на моделях і на експериментальних макетах нові пристрої, які базуються на оригінальних принципах (Рис. 9).
 |
| Рис.9. Оригінальні пристрої НВЧ діапазону, створені у відділу №12 |
Колектив відділу завершив роботу над другою версією системи моделювання – МWD-02, що має засоби для специфікації і редагування конфігурації об’єкта на базі AutoCAD, і призначеної для аналізу, оптимізації та візуалізації електродинамічних характеристик антено-фідерних пристроїв та резонансних систем на базі найрізноманітніших трактів від прямокутних, круглих, коаксіальних та багатопровідних ліній аж до нових ліній дуже складних екзотичних перетинів, що виникають у процесі розрахунків. В основі нової інтерактивної системи лежать, насамперед, проблемно- орієнтовані чисельно-аналітичні методи розв’язання крайових задач, що забезпечують найвищу точність та швидкість обчислень у своїх класах конфігурацій, використання різних алгоритмів оптимізації від градієнтних до генетичних і сучасні об’єктно-орієнтовані методи програмування.
Останні 10 років зусилля співробітників відділу сфокусовані на узагальнюючому підході до розв’язку векторних крайових задач хвилевідної електродинаміки. Цей підхід був алгоритмізований, реалізований, налагоджений і верифікований на широкому спектрі різноманітних практичних та фундаментальних задач. Важливо відзначити, що як прикладні, так і фундаментальні дослідження стало можливим проводити в рамках єдиного програмного комплексу MWD. Триває розробка математичних моделей і відповідних програмних кодів для аналізу хвилеводів з довільними гладкими межами і їх фрагментів. Виконано програмну реалізацію алгоритмів розрахунку спектрів власних хвиль об’єктів з кусково-координатними декартовими і циліндричними межами (методом часткових областей з урахуванням особливостей), а також гладкими границями (методом інтегральних рівнянь) і методу ступінчастої апроксимації у задачах про вузли з некоординатними межами. На основі методу узагальнених матриць розсіяння реалізовано організацію електродинамічної збірки при розрахунку складних хвилеводних об’єктів з урахуванням симетрії структур. Обчислення, аналіз та синтез тривимірних систем доповнений градієнтною і ройовою оптимізаційними процедурами [23-29] (А.В. Борискін, Н.Г. Дон, Д.Ю. Кулик, С.Ф. Кулішенко,А.О. Кириленко, А.О. Перов; С.А. Приколотін, Л.А. Рудь, С.О. Стешенко, С.Л.Сенкевич, В.І.Ткаченко).
Розрахунок та синтез композиційно складних вузлів антено-фідерних трактів
На основі розроблених алгоритмів було вирішено задачі синтезу ряду композиційно-складних хвилеводних вузлів, серед яких слід виділити:
- поляризаційні діплексери із загальним круглим хвилеводом і поляризаційні діплексери на коаксіальних та гребінчатих хвилеводах (Д.Ю. Кулик, А.О. Кириленко, А.О. Перов, Л.А. Рудь, С.О. Стешенко, С.Л. Сенкевич, В.І. Ткаченко) [30,31];
- перетворювачі TE10–TEq0 типів хвиль на несиметричних куточках у прямокутному хвилеводі (А.О. Кириленко, Л.А. Рудь) [32];
- збудники типів хвиль (ТЕ11 и ТЕ01) в коаксіальному хвилеводі, включеному до складу відкритого резонатора (Л.А. Рудь, І.К. Кузьмічов (відд. №11)) [33];
- надкомпактні 90-градусні скрутки в прямокутних хвилеводах (А.О. Кириленко, Д.Ю. Кулик, Л.А. Рудь) [34];
- антени витекаючих хвиль з завданим розподілом поля на апертурі та перетворювачі поверхневих хвиль в об’ємні на тривимірних уповільнюючих системах (А.О. Кириленко, С.О. Стешенко) [35,36];
- компактні інтегральні діелектричні лінзові антени з оптимізованими профілем і робочими характеристиками (А.В. Борискін) [37,38].
Оригінальна конструкція перетворювача типів хвиль [32], що забезпечує ефективне узгодження і рівномірний розподіл НВЧ потужності при розігріві, вже використовується на Дружківській фаянсовій фабриці (Україна).
Важливим досягненням цього напрямку є розробка антенного блока для охолоджуваного тридіапазоного (S/X/Ka) коаксіального випромінювача дзеркала радіотелескопа ([39], (А.О. Кириленко, Д.Ю. Кулик, А.О. Перов, С.А. Приколотін, Л.А. Рудь, С О. Стешенко). Роботу виконано в рамках міжнародного проекту VLBI2010 у співпраці з групою В.М. Скресанова (відділ №24), вона фінансувалася НВО «Сатурн» (м.Київ) та НАНУ за конкурсною НДР «КОСМОС».
Узагальнення спектральної теорії відкритих хвилеводних резонаторів на хвильові та періодичні резонатори тривимірної (3D) геометрії
УСТ ВХР було використано для встановлення фізичної природи резонансних ефектів в тривимірних хвилеводних структурах і перфорованих екранах: резонансного віддзеркалення тонким вертикальним або горизонтальним провідником зі зламом (А.О. Кириленко, С.А. Приколотін) [40,41], прямокутними стрижнями (А.О. Кириленко, Л. П. Мосьпан) [42] в прямокутному хвилеводі; резонансного поглинання несиметричними діелектричними вставками в прямокутному хвилеводі (Л.А. Рудь) [43], «екстраординарного» проходження (enhanced transmission) крізь гратки з малими отворами і резонансні ефекти в компаундних гратках (А.О. Кириленко, Н.Г. Дон (Колмакова), А.О. Перов) [44,45].
На низці 3D об’єктів продемонстровано існування «сплячих коливань», що не мають радіаційних втрат і проявляють себе сплесками АЧХ при порушенні тієї чи іншої симетрії: площинної, обертальної або трансляційної. З іншого боку, вперше продемонстровано, що плоскі хвильові елементи або двовимірні гратки з них (з дуже малим реальним об’ємом) можуть мати коливання з добротністю, обмеженою лише омічними втратами, коли резонансні ефекти не пов’язані з будь-якою симетрією об’єкта або з її порушенням. Вони зобов’язані своїм існуванням лише спеціальній геометрії об’єкта і шестикомпонентності електромагнітного поля (А.О. Кириленко, Л П. Мосьпан, Н.Г. Дон (Колмакова), А.О. Перов).
Досліджено «електродинамічну» природу явища «оптичної активності» в метаматеріалах, що сформовані з граток періодично розташованих смугово-киральних комірок та шарів діелектрика, а також в складних хвилеводних об’єктах, що мають обертальну симетрію четвертого порядку (Н.Г. Дон, А.О. Кириленко, А.О. Перов, С.А. Приколотін, С.Л. Просвірнін (РІ АН)) [46-48]. Встановлено, що перетворення об’єкту з декартово-симетричного на С2(4) симетричний «смугово-киральний», веде до повороту площини поляризації дише при наявності додаткового об’єкта в ближньому полі. Найбільший ефект дають «зв’язані» об’єкти, що забезпечують D2(4) симетрію у цілому. Виникаючі при цьому власні коливання забезпечують і найвищу «оптичну активність» і повне узгодження.
Найбільш значущими результатами в рамках УСТ ВХР є виявлення «апертурних» коливань, відповідальних за явища повного проходження через позамежні отвори або через їх періодичні системи (навіть при ідеальній провідності!) [44,49,50], а також аналіз нових D4(2)-симетричних коливань в сполучених смугово-киральних об’єктах [46,48,51] (Н. Г. Дон, А. О. Кириленко, А. О. Перов, С. А. Приколотін). Виявлено зони зближення власних частот останніх, що породжують широкі смуги прозорості об’єктів при високій «оптичній активності».
Розробка пристроїв, що працюють на нових принципах. Від дослідження фізики процесів до реального пристрою
В рамках цього напрямку було запропоновано ряд оригінальних пристроїв НВЧ діапазону (Рис.10). Багатоапертурні стрічкові відбивні комірки в прямокутному хвилеводі1, фільтри гармонік і фільтри з внесеними полюсами затухання. Багатоапертурні гратки та частотно-селективні поверхні з внесеними полюсами загухання на АЧХ [52-55] (А.О. Кириленко, Л.П. Мосьпан). Багатоапертурні відбивні комірки в циліндричному хвилеводі1 [56] (Н.Г. Дон, Л.П. Мосьпан, А.О. Кириленко). Поглинаючі ячейки на основі хвилеводно-діелектричних резонаторів з одностороннім прямокутним виступом (Л.А. Рудь) [57]. Резонансні відбивні комірки на основі хвилеводної секції з двома стрижнями [58]. Хвилеводний елемент синглетного типу1 (Л.П. Мосьпан, А.О. Кириленко) [42]. Тонкий провідник із ступінчастим зламом в поперечному перерізі прямокутного хвилеводу як простий відбивач1 [40] (А.О. Кириленко, С.А. Приколотін). Хвилеводна діафрагма з вертикальною ступінчастою щілиною [41] (А.О. Кириленко, С.А. Приколотін). Обертувачі площини поляризації на довільний кут на основі планарних киральних діафрагм2 [47,48] (Н.Г .Дон (Колмакова), С.А. Приколотін, Л.А. Просвірнін (РІ АН)). Киральні гратки2 [51] (Н.Г. Дон, А.О. Кириленко, С.А. Приколотін). Результати чисельного моделювання підтверджені експериментально у відділах №12(1) (Є.А. Свердленко) та №18(2) (В М. Деркач).
 |
| Рис.10. Оригінальні НВЧ пристрої, створені у відділі №12 [34,40, 42, 44, 51,56 ] |
ЛІТЕРАТУРА
- Кириленко А.А., Масалов С.А., Шестопалов В.П., Принцип взаимности и некоторые физические закономерности рассеяния волн на дифракционных решетках // Вестник АН УССР. ‑1975. ‑ 11, №3.
- Кириленко А.А., Масалов С.А., Шестопалов В.П., Сиренко Ю.К., Резонансное рассеяние волн т.1. Дифракционные решетки, «Наукова думка». ‑ 1986. 232 c.
- Kirilenko A., Mospan L., Perforated strips as rejection FSS // Proc. of Int. MMET2004, Sept., 14-17, Dnepropetrovsk, Ukraine. – 2004. ‑ pp 359-341.
- Kirilenko A.A., Rud‘ L.A., Tkaсhenko V.I., Angled bend Hqо-mode exciters // Conf.Proc. of 24‑th Europ. Microwave Conf.,1994, Cannes, V.1. ‑ pp.284-288.
- Кириленко А.А., Рудь Л.А., Шестопалов В.П., Резонансное рассеяние волн. T.2. Волноводные неоднородности // Монография, K.: изд. «Наукова думка», 1986, 216 c.
- Рудь Л.А., Спектральный метод в задаче согласования неоднородностей в многомодовых волноводах // Докл. АН УССР. Сер. А. – 1987. – № 10. – сc.46-49.
- Рудь Л.А., Сиренко Ю.К., Яцик В.В., Яшина Н.П., Спектральный метод анализа эффектов полного преобразования волн открытыми периодическими и волноводными резонаторами // Изв. вузов. Радиофизика. 1988. – T.31, № 10. – cc.1246–1252.
- Kirilenko A.A., Tysik B.G., Connection of S-matrix of waveguide and periodical structures with complex frequency spectrum. // Electromagnetics. – 1993. – V.13, N3. – pp. 301–318.
- Kirilenko A.A., Mospan L.P., The simplest notch and bandstop filters based on the slotted strips // Conf. proc. of EUMC-31, London, 27-27 Sept. 2001,V.1 pp.117-120.
- Кириленко А.А., Сенкевич С.Л., Новый тип добротных колебаний в открытых волноводных резонаторах // Письма в ЖТФ. – 1986. – Т.12, вып. №14. – cс.876–879.
- Minakova L.B., Rud L.A., Resonance absorption in single and cascaded lossy waveguide-dielectric resonators // Microwave and Optical Technology Letters. – 2003. – V.36, No.2. – pp.122–126.
- Zinenko T.L., Nosich A.I., Okuno Y., Plane wave scattering and absorption by resistive-strip and dielectric-strip periodic gratings // IEEE Trans. Antennas and Propagation. – 1998. ‑ V. AP-46, no.10. ‑ pp.1498-1505.
- Kirilenko A.A., Fisun A.I., Tkachenko V.I., Belous O.I., Exact simulation of 2-D open resonant system with echelette mirrors // Proc. of 25-th European Microwave Conf. Sept. 4-7, Bologna, Italy, 1995.
- Nosich A.I., Radiation conditions, limiting absorption principle, and general relations in open waveguide scattering // Electromagnetic Waves and Applications. – 1994. ‑ V.8, no.3. ‑ pp.329-353.
- Boriskina S.V., Benson T.M., Sewell P., Nosich A.I., Highly efficient full-vectorial integral equation solution for the bound, leaky, and complex modes of dielectric waveguides // IEEE J. on Selected Topics in Quantum Electronics. ‑ 2002, V.8, No.6. ‑ pp.1225-1232.
- Boriskin A.V., Nosich A.I., Whispering-gallery and Luneburg lens effects in a beam-fed circularly-layered dielectric cylinder // IEEE Trans. Antennas and Propagation. – 2002. ‑ Vl.AP-50. – no.9. ‑ pp.1245-1249.
- Rondineau S., Nosich A.I., Daniel J.-P., Himdi M., Vinogradov S.S., MAR-based analysis of a spherical-circular printed antenna with a finite ground excited by an axially-symmetric probe // IEEE Trans. Antennas and Propagation. – 2004. ‑ V.AP-52, No.5. ‑ pp.1270-1280.
- Кириленко А.А., Масалов С.А., Шестопалов В.П., Матричные уравнения типа свертки // Монография, K.: изд. «Наукова думка», 1984, 296 c.
- Kirilenko A.A., Kulik D., Rud L., Tkachenko V., P.Pramanick, Electromagnetic modeling of multi-layer microwave circuits by the longitudinal decomposition approach, MTT-S Symp. Digest, May 20-24, Phoenix, Arizona, USA, 2001, pp.1257-1260.
- Kirilenko A.A., Kulik D., Rud L., Tkachenko V., P.Pramanick, Electromagnetic modeling of multi-layer microwave circuits by the longitudinal decomposition approach, MTT-S Symp. Digest, May 20-24, Phoenix, Arizona, USA, 2001, pp.1257-1260.
- Kirilenko A.A., Orlov M.V., Tkachenko V.I., Stepped model of smooth irregularities corrected for location of equivalent reflection surface // Electronic Letters. – 1993. – V.29, N25. – pp.2180–2181.
- Kirilenko А.А., Kulishenko S.F., Kulik D.Yu., Senkevich S.L., Calculation of waveguide discontinuities with smooth boundaries using mode matching technique //Conf. Proc. оf MMET-2004, Dniepropetrovsk, Ukraine, Sept. 14-17. – 2004. ‑ pp.139-141.
- Кириленко А.А., Ткаченко В.И., Сенкевич С.Л., Кулишенко С.Ф. Организация «электродинамической» сборки при расчете сложных волноводных объектов // Радиотехника и электроника. – Х., –T.52, №6. ‑cc.679‑686.
- Кириленко А.А., Сенкевич С.Л., Стешенко С.А. Анализ трехмерных замедляющих систем на основе метода обобщенных матриц рассеяния // Радиофизика и электрон.: cб. науч. тр. // Ин-т радиофизики и электрон. НАН Украины. – Х., 2008. – T.12, спец. выпуск. ‑cc. 122‑129.
- Приколотин С. А., Кириленко А.А., Метод частичных областей с учетом особенностей во внутренних задачах с произвольными кусочно-координатными границами. Часть 1. Спектры собственных волн ортогонных волноводов // Радиофизика и электрон.: cб. науч. тр. // Ин-т радиофизики и электрон. НАН Украины. – Х. – – T.15, №2. – cc.17‑29.
- Стешенко С.А., Приколотин С.А., Кириленко А.А., Кулик Д.Ю., Рудь Л.А., Сенкевич С.Л., Метод частичных областей с учетом особенностей во внутренних задачах с произвольными кусочно-координатными границами. Часть 2. Плоско-поперечные соединения и «in-line» объекты // Радиофизика и электрон.: cб. науч. тр. // Ин-т радиофизики и электрон. НАН Украины. – Х., 2013, T.4(18), №1. –cc.15‑25.
- Steshenko S.A., Prikolotin S.A., Kulik D.Yu., Kirilenko A.A., Mospan L.P., Rud L.A., Numerical determination of eigenmodes of an arbitrary waveguide with coordinate boundaries in cylindrical coordinate system // Int. Symp. on MSMW’13 [Электронный ресурс]: Proc. ‑Kharkiv, 2013. – 1 эл. опт. диск (CD‑ROM). – Загол. з етікетки диска.
- Don N., Kirilenko A.A., Germani S., Bozzi M., Perregrini , Determination of the mode spectrum of arbitrarily shaped waveguides using the eigenvalue-tracking method // Microwave and Optical Tech. Lett. ‑ 2006, V.48, № 3. –pp.553-556.
- Galan A.Yu, Sauleau R., Boriskin A.V., Floating boundary particle swarm optimization algorithm // Optiс – 2013. –V.7, № 6. – pp.1261–1280.
- Herscovici N., Kirilenko A.A., Kulik D.Yu., Rud L.A., Tkachenko V.I., Electromagnetic Modeling and Design of Dual-Band Septum Polarizers // Applied Comp. Electromagnetics Society Journal. – 2006. –V.21, № 2. ‑ Р. 155‑163.
- Перов А. О., Рудь Л.А., Ткаченко В.И., Поляризационные диплексеры с общим круглым волноводом // Радиотехника и электроника. – 2007. – T.52, №6. – cc.671‑678.
- Kirilenko A. A., Rud L.A., Nonsymmetrical H-plane corners for TE10–TEq0-mode conversion in rectangular waveguides // IEEE Trans. on MTT. – 2006. ‑54. №6, pt. 1. ‑ pp.2471‑2477.
- Кузьмичев И.К. Возбуждение ТЕ11 и ТЕ01 волн в коаксиальном волноводе, включенном в состав открытого резонатора. Часть 2. Моделирование ключа // И.К.Кузьмичев, А.Ю.Попков, Л.А.Рудь // Физические основы приборостроения, 2012, т. 1, №4, c93-101.
- Kirilenko A. A., Kulik D.Yu., Rud L.A., Compact 90o twist formed by a double-corner-cut square waveguide section / // IEEE Trans. on MTT. ‑ 2008. –V.56, №7. ‑ pp.1633‑1637.
- Kirilenko A., Steshenko S., Analysis and optimization of planar antenna based on finite reflection grating fed by a dielectric waveguide // EuCAP’2006 [Електрон.]: Proc. ‑Nica, 2006. – 1 эл.опт. диск (CD‑ROM). – Загл. с этикетки диска.
- Стешенко С. А. Синтез антенны вытекающих волн по заданному распределению поля на апертуре // Радиофизика и радиоастрономия. — 2013. — T.8, № 4. ‑ cc.373‑380.
- Boriskin A. V., Zhadobov M., Steshenko S., Drean Y.Le, Pearson C., Sauleau R., Enhancing exposure efficiency and uniformity using a choke ring antenna: application to bioelectromagnetic studies at 60 GHz // IEEE Trans. on MTT. ‑2013‑V.61, №5. ‑ pp.2005‑
- Rolland A., Ettorre M., Boriskin A.V., Le Coq L., Sauleau R., Axisymmetric resonant lens antenna with improved directivity in Ka-band / // IEEE Antennas Wireless Propag. Lett. – 2011. –V.10, №.1, prt. ‑pp. 37–40.
- Ипатов А.Б., Чмиль В.М., Скресанов В.Н., Иванов Д.В., Мардышкин В.В., Чернов В.К., Пилипенко А.М., Кириленко А.А., Криогенный приемный фокальный блок для телескопов радиоинтерферометрического комплекса нового поколения // Радиофизика и радиоастрономия. — 2014. — Т. 19, № 1. — cc.81-96.
- Prikolotin S. A novel notch waveguide filter / S. Prikolotin, A. Kirilenko // Microwave and Optical Tech. Let. – 2010. –V.52, Iss. 2. – pp.416‑420.
- Prikolotin S., Kirilenko A. Waveguide bandstop (bandpass) filters on stepped conductors (slots) sections / // EuMW’2011 [Електрон.]: Proc. ‑ Manchester, UK 9-14 Oct., 2013. – 1 эл.опт. диск (CD‑ROM). – Загл. c этикетки диска.
- Mospan L. P., Prikolotin S.A., Kirilenko A.A., Singlet Formed by Two Transversal Ridges in a Rectangular Waveguide from the Spectral Theory Point of View // EuMW’2013 [Электронный ресурс]: Proc. ‑Nuremberg, Gr., 2013. – 1 эл.опт. диск (CD‑ROM). Загол. з етікетки диска.
- Рудь Л. А. Поглощение в волноводно-диэлектрических резонаторах с односторонним прямоугольным выступом // Радиофизика и электроника: Сб. научн. тр. / ИРЭ НАН Украины. – 2007. –V.12, №2. ‑ cc.299‑305.
- Kirilenko A. A., Perov A.O., On the common nature of the enhanced and resonance transmission through the periodical set of holes / // IEEE Trans. on AP. – 2008. –V.56, №10. – pp.3210‑3216.
- Перов А.О., Кириленко А.А., Сенкевич С.Л. Собственные колебания и резонансные свойства одномерно-периодических решеток из металлических брусьев Часть 2. Компаундная решетка / // Радиофизика и электроника. – 2013. –V.4(18), №1. ‑ cc.15-25.
- Кириленко А.А., Колмакова (Дон) Н.Г., Перов А.О., Приколотин С.А., Деркач В.Н., Cобственные колебания, обеспечивающие поворот плоскости поляризации на 900 с помощью планарных киральных двухщелевых диафрагм // Изв. ВУЗов. Радиоэлектроника. – 2014 –T.57, №12. ‑ cc.3‑15.
- Колмакова Н, Кириленко А., Просвирнин С., Плоскo-киральные диафрагмы в квадратном волноводе и проявления «оптической активности» // Радиофизика и радиоастрономия. – 2011. –T.16, №1 ‑cc.70‑81.
- Приколотин С.А., Кириленко А.A., Колмакова Н.Г., Сверхкомпактная 90° скрутка на основе пары плоско-киральных диафрагм в квадратном волноводе // Известия ВУЗов. Радиоэлектроника. – 2012. –V.55, №4.‑ cc.31–35.
- Дон Н.Г., Перов А.О., Сенкевич С.Л., Кириленко А.А., Аномальное прохождение ЭМВ сквозь запредельные отверстия и собственные колебания волноводных объектов и периодических структур // Изв. вузов. Радиоэлектроника – 2011. –T.54, №3. ‑ cc.3‑13.
- Дон Н. Г., Кириленко А.А., Сенкевич С.Л., Новый тип собственных колебаний и резонанс полного прохождения через диафрагму с запредельным отверстием в прямоугольном волноводе // Известия вузов. Радиофизика. – 2008. ‑51, №2 ‑ с. 111‑115.
- Derkach, Kirilenko А., Salogub А., Prikolotin S., Kolmakova N., Ostrizhnyi Ye., Gigant optical activity in artificial plane-chiral structures // [Електрон. ресурс]: Proc. ‑Kharkiv, 2013. – 1 эл.опт. диск (CD‑ROM). – Загол. з этикетки диска.
- Кириленко А. А., Мосьпан Л.П., Ткаченко В.И., Многощелевые диафрагмы как инструмент управления амплитудно-частотной характеристикой (физика и применения, обзор результатов) // Радиотехника и электроника. ‑ 2005. –T.50, №2. ‑ cc.1‑10.
- Kirilenko A.A., Mospan L.P., A slotted strip as a key element of the simplest notch and bandstop filters // Microwave and Opt. Tech. Letters. – 2005. –V.46, Iss.1. ‑ pp.20‑24.
- Mospan L.P., Kirilenko A.A., Spatial Filter with Quasi-Elliptical Response // EUMW’2005 [Электронный ресурс]: Proc. ‑Paris, 2005. – 1 эл.опт. диск (CD‑ROM). – Загл. с этикетки диска.
- Kirilenko A.A., Mospan L.P., Grating of зerforated strips as a multi-rejection FSS // IEEE APS [Электронный ресурс]: Digest. –Phoenix, 2005, – 1 эл. опт. диск (CD‑ROM). – Загл. с этикетки диска.
- Don N., Mospan L., Kirilenko A., Layout of a multislot iris as a tool for the frequency response control // Microwave and Tech. Lett. – 2006. –V.48, Iss.8. ‑ pp. 1472‑1476.
- Rud L.A., Resonance absorption in nonsymmetrical lossy dielectric inserts in rectangular waveguides // IEEE Trans. on MTT. – 2007. – V.55, №8. ‑ pp.1717‑
- Кириленко А.А., Кулик Д.Ю., Мосьпан Л.П., Л.А.Рудь, Резонансы отражения волноводной секции с двумя разновысокими стержнями // Радиофизика и электроника: Сб. научн. тр. / ИРЭ НАН Украины. – –T.13, №2. ‑ cc.154‑158.

 15.06.2016
15.06.2016